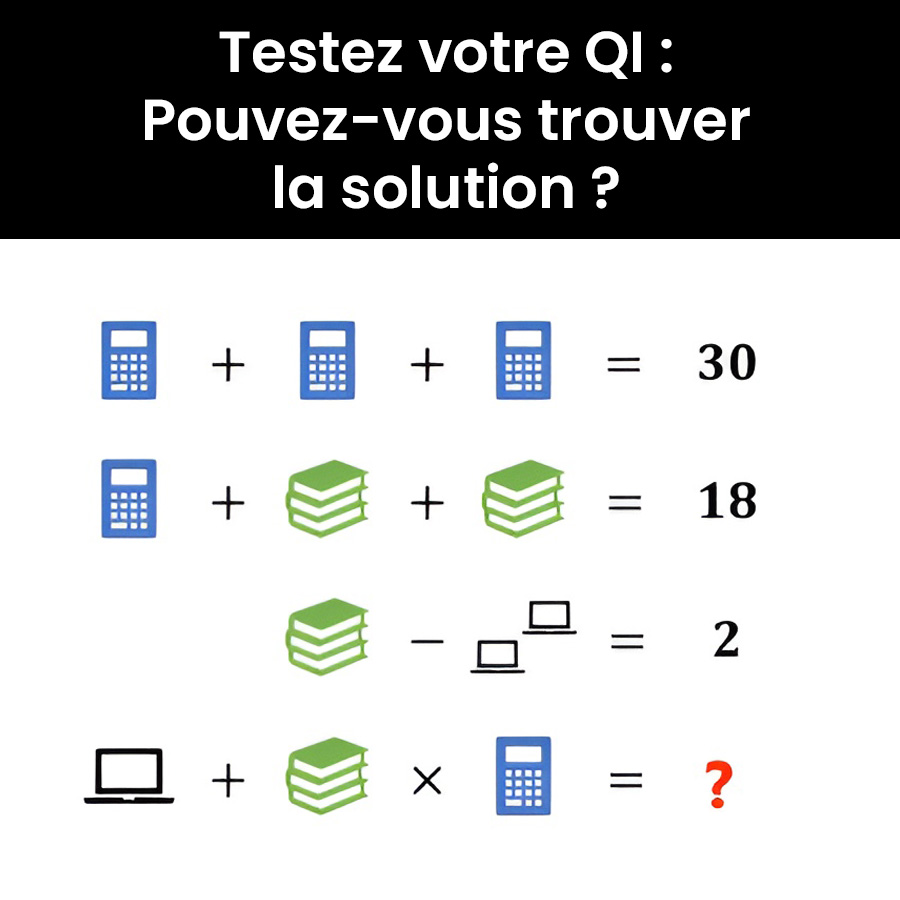
Tout commence par un simple tweet du ministre de l’Éducation argentin, Nicolás Trotta, partageant un problème mathématique. Ce casse-tête, devenu rapidement viral, a divisé les internautes entre plusieurs solutions possibles. Mais pourquoi un problème apparemment simple suscite-t-il autant de débats ?
Le problème
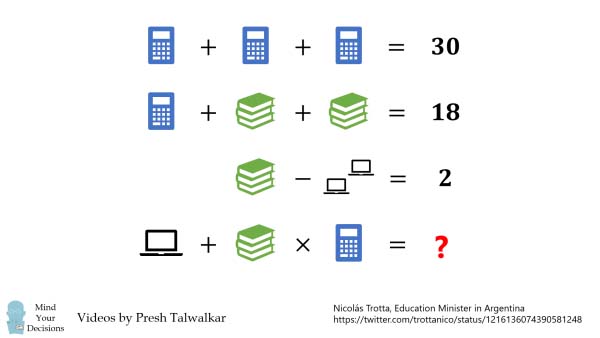
Imaginez une équation où des objets du quotidien comme calculatrices, livres et ordinateurs portables remplacent les nombres. Votre mission ? Trouver la valeur de chaque objet tout en respectant l’équilibre de l’équation. Facile, non ? Pas si sûr !
Ces énigmes visuelles nécessitent une attention particulière, car chaque détail compte :
Les symboles se ressemblent, mais ne sont pas identiques. Par exemple, un livre peut avoir un nombre de pages différent, ou une calculatrice afficher un écran distinct.
Les opérations sont classiques, mais la solution réside dans votre capacité d’observation minutieuse.
Résolution du problème
Commençons par définir les variables :
CC représente une calculatrice,
BB un ensemble de livres,
LL une paire d’ordinateurs portables,
xx un seul ordinateur portable.
Les équations fournies sont les suivantes :
C+C+C=30C+C+C=30
C+B+B=18C+B+B=18
B−L=2B−L=2
x+B×C=?x+B×C=?
Étape 1 : Résolvons pour CC à partir de la première équation.
C+C+C=30C+C+C=30
3C=303C=30
C=10C=10
Étape 2 : Résolvons pour BB à partir de la deuxième équation.
C+B+B=18C+B+B=18
10+2B=1810+2B=18
2B=82B=8
B=4B=4
Étape 3 : Résolvons pour LL à partir de la troisième équation.
B−L=2B−L=2
4−L=24−L=2
L=2L=2
Étape 4 : Résolvons pour xx.
Sachant que L=2L=2 correspond à une paire d’ordinateurs portables, il est logique d’interpréter cela comme :
2=L=x+x2=L=x+x
x=1x=1
Nous pouvons alors évaluer l’expression suivante :
x+B×Cx+B×C
=1+4×10=1+4×10
=1+40=1+40
=41=41
C’était la solution officielle !
Pourquoi tant de confusion ?